Recently I was trying to explain to my daughter about the concept of digital signature, and obviously the term Hashing popped up. Later I realized not only kids but even many grownups have trouble grasping the concept of digital signature and cryptography in general. So thought of writing a series of blogs and try to explain the related concepts for the beginners. In the process I also ended up writing some code to a small utility to convert any text to a Hash. Do drop in your comments.
Hashing is a crucial concept in computing and cybersecurity, providing a means for ensuring data integrity, securely storing passwords, and supporting various cryptographic operations.
Hashing or better known as Hashing Algorithm is a mathematical formula, which convert an input (or “message”) of any length, into a fixed-size string of bytes, typically called a digest, fingerprint that appears random.
Please take a look at a simple implementation of the Hashing utility
So, what is Hashing?
The simplest explanation is that Hashing is a cryptographic process that transforms any input data, such as text or files, into a fixed-size string of characters, typically a unique series of numbers and letters. This output, known as a hash value or hash code, is generated using specific algorithms like MD5, SHA-1, or SHA-256.
Practical use of Hashing
Hashing is widely used for verifying data integrity, securing passwords, and ensuring the authenticity of messages and files by making sure that even the slightest change in the input results in a drastically different hash. It is essential in cybersecurity and data management due to its efficiency and reliability.
Hashing is used in the following, but not limited to it:
-
- Password verification.
- Blockchain and Cryptography.
- Data Integrity (Checksums and Hashing Algorithms)
- Data Storage and Retrieval (Hash Tables / Hash Maps)
- Content Addressing (Git and Version Control Systems)
- Caching systems.
- Image, Audio, and Video Processing
- URL Shortening (like bit.ly)
An Example of Hashing Algorithm
Let’s take a look at an example of a simple algorithm to understand the concept.
Lets say we have to Hash the word “world” using an algorithm we formulated.
Our algorithm adds up the position of all alphabets in the input text and produces an output number.
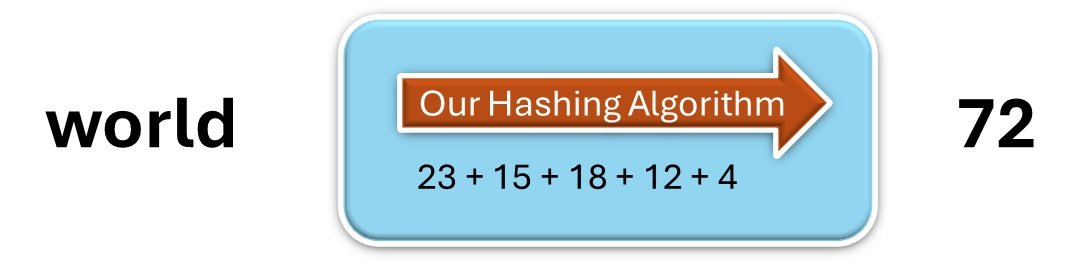
In this case the word “world” consists of five alphabets, where “W” is the 23rd alphabet and “O” is 15th Alphabet and so on…and the output number is 72.
Here the output number 72 represents the word “world”. Result of hashing algorithm is called Digest, it is also called Checksum, Fingerprint, Hash, CRC etc. in the industry.
For the time being let’s call the output as Digest. in this case the input message is “world” and the message Digest is “72” after using the above hashing algorithm.
The purpose of the message Digest is to use the digest to compare two digest to check if they came from the same input message.
For example lets make a small change in the input message from “world” to “warld”.
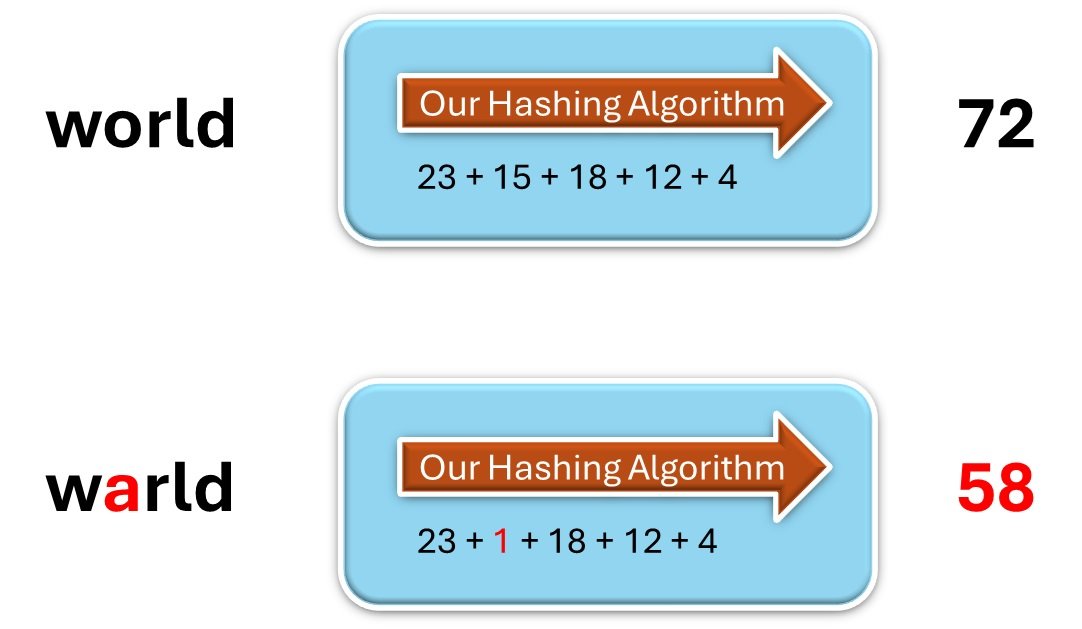
The output message Digest will be different and now we can compare the two Digests “72” and “58” and conclude that the Digests came from two different input messages.
Key Characteristics Of Hashing Algorithm
Our hashing algorithm is a weak hashing algorithm, in real world this algorithm cannot be used for any meaningful scenario.
In order for a Hashing Algorithm to meet the industry standard, the algorithm should satisfy basic requirements:
-
Infeasibility:
Infeasible to generate a given Digest. That means, no one can generate the same Digest without knowing the original input message.
(In this case the digest “72”, can be re-produced by anyone within few minutes of effort. There can be more than four to five words that can generate the digest “72”. This is also called Hash Collision. Hence our algorithm is not usable in real world. In real world this should be so difficult that it should be impossible to do it.)
-
One Way Encryption:
It should be impossible to extract the original input message from the Digest. This is also called one way encryption, which means we can encrypt input message to a digest but cannot decrypt a digest to the original message.
(In our case if we give someone the Digest value “72” it will be impossible to reverse engineer the input message “world”, actually our algorithm does meet this criteria. Even if there can multiple words that can produce the Digest “72”.)
-
Avalanche Effect:
A small change in the input message should produce a significantly different Digest. The difference in the digest should not give any hint about the amount of change in the original messages. This is also called the Avalanche Effect on the digest.
(In our case the difference between the two digests “72” and “58” are not that significant, people can guess the change in the original message is very less. Hence our algorithm is not usable in real world.)
-
Fixed-Length Output:
The Hashing algorithms should produce a fixed-length Digest, regardless of the size of the input message.
(In our case we got both the digests “72” and “58” with two-digit length, that is probably our input message is of same length. However, if we give a full paragraph as input message, our Digest length will increase. Hence our algorithm is not usable in real world.)
There are other conditions that an efficient advanced Hashing Algorithm also supports, but the above are the primary conditions.
Understand Hash Collision
When two input messages are producing identical Digest, it is called Hash Collision. This is a serious problem for some of the practical usage of Hashing. However, this cannot be avoided, as it is a byproduct of the fixed length of a Digest.
Many robust Hashing algorithm has been breached over the years of usage of the algorithm.
Let’s understand Hash Collision with an example.
Let us assume we have a new Hash Algorithm with produces Digest of three bits. So how many digests such a system can produce? As in a bit we can store either “0” or “1”. So, we can maximum have 8 unique combinations of “0” and “1” to represent out Digests.
Here is all the possible combination of our Digest:
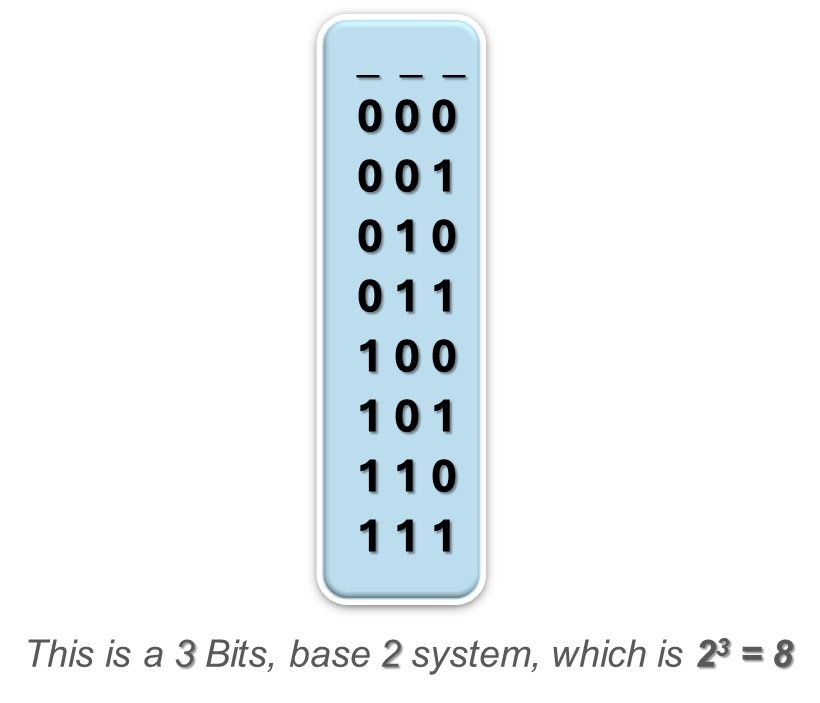
In this case the length of the Digest will be 3 Bits, which is very small as a binary system with is base 2 can produce only 8 Digests. In real world the length should be above 100 bits to have some usable range of Digest.
The fact that, in such a hashing system there can be only 8 possible Digests, suggests that there will be only 8 unique input messages that will get unique corresponding Digest.
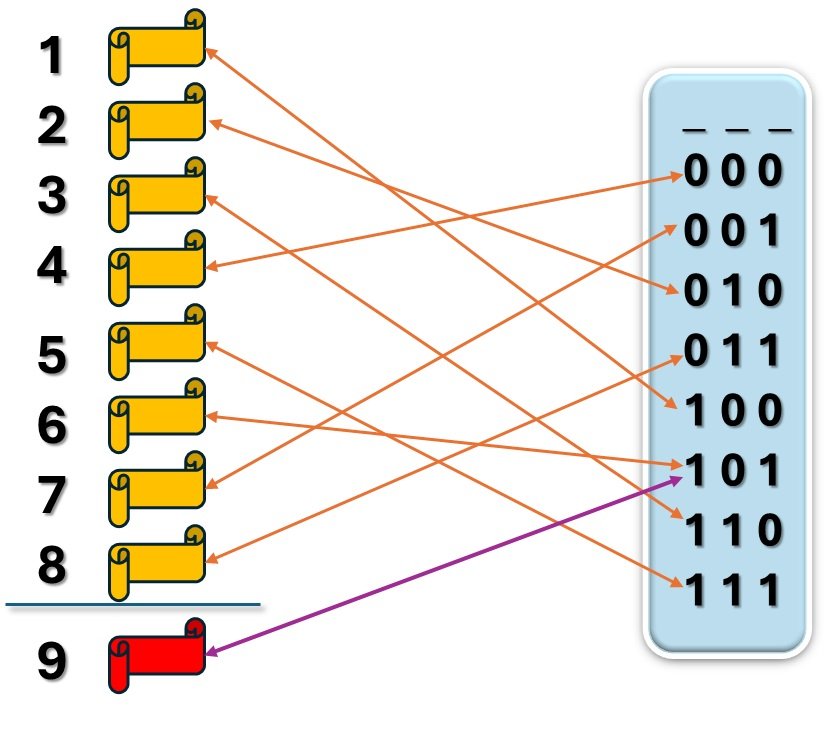
Now if we try overuse this algorithm to Hash the 9th message it will reuse one of the used Digest. That is why we cannot avoid Collision in practical term, but we can make it absolutely rare by increasing the length. Higher Bit output Digest are rarely going to hit Collision.
Message Integrity – A practical use of Hashing
Lets say there are two person “A” and “B”. “A” wants to send a message to “B”.
To keep things simple, for the time being let’s consider the message is not a secret message.
One of the objectives is to ensure that the message was not changes while in transit. In other word, to ensure data integrity.
Hashing can be used in this scenario. Let’s see how.
1) Person “A” can pass the Message through a Hashing algorithm (MD5, SHA etc.) and generate a Digest.
2) Person “A” sends both the Message and the Digest to Person “B”.
3) Once “B” receives the message, separates the Message and Digest for future reference,
4) “B” generates a new Digest using the same algorithm.
5) If the two Digests matches, then we can conclude that the message was not changed during transit.

Of course, there are flaws in this over-simplified scenario. If someone captures the message during transit and changes the message, as well as generates a corresponding Digest using the same algorithm and sends the message to the target person “B”, then “B” will not be able to tell doing the above steps if the message was changed in transit.
There is other technique to address that we will explain in a separate article in “What is HMAC and how does it secure data” (Hash-based Message Authentication Code). But as of now this is what Hashing do at its core.
The Common Hash Algorithm
Today we have quite a few Hashing Algorithm, few of the common algorithm are listed below:
| Hash Algorithm | Bit Length | Status | Use Cases | Security |
|---|---|---|---|---|
| SHA-1 | 160 bits | Deprecated (insecure) | Previously used in SSL/TLS, digital signatures | Collision vulnerabilities, not recommended |
| SHA-224 | 224 bits | Secure | Digital signatures, certificates | Secure |
| SHA-256 | 256 bits | Secure | Digital signatures, blockchain, certificates | Secure, widely used |
| SHA-384 | 384 bits | Secure | Digital signatures, certificates | Secure |
| SHA-512 | 512 bits | Secure | Digital signatures, high-security applications | Secure |
| SHA-3 | 224, 256, 384, 512 bits | Secure | Alternative to SHA-2, advanced cryptographic applications | Secure |
| MD5 | 128 bits | Broken (insecure) | Legacy checksum, file integrity (non-secure) | Collision attacks, not recommended |
| MD4 | 128 bits | Obsolete (insecure) | Rarely used | Broken |
| RIPEMD-160 | 160 bits | Secure | Blockchain, digital signatures | Secure |
| RIPEMD-128 | 128 bits | Insecure | Older applications | Collision vulnerabilities |
| RIPEMD-256 | 256 bits | Secure | Cryptographic applications | Secure |
| BLAKE2b | Variable (up to 512 bits) | Secure | File integrity checks, digital signatures | Highly efficient, secure |
| BLAKE2s | 256 bits | Secure | File integrity, cryptographic applications | Highly efficient, secure |
| BLAKE3 | 256 bits | Secure | Cryptographic applications requiring high performance | Fast, secure, scalable |
| Whirlpool | 512 bits | Secure | Digital signatures, file hashing | Secure |
| Tiger | 192 bits | Secure | Backup systems, integrity checks | Fast, but less common |
| bcrypt | Variable (184 bits typical) | Secure | Password hashing | Slow, resistant to brute-force attacks |
| scrypt | Variable | Secure | Password hashing, cryptocurrency mining | Memory-hard, resistant to hardware attacks |
| Argon2 | Variable | Secure | Password hashing | Highly secure, winner of Password Hashing Competition |
| CRC (Cyclic Redundancy Check) | Varies (8, 16, 32 bits) | Not secure (non-cryptographic) | Data integrity in non-cryptographic applications | Used for error detection, not security |
| FNV (Fowler-Noll-Vo) | 32, 64 bits | Not secure (non-cryptographic) | Hash tables, non-cryptographic applications | Not secure, used for performance in data structures |
Please take a look at a simple implementation of the Hashing utility